What's Math Got to Do With It?

Why does my child's math look so different than the way I learned it? A common question I hear in conversations. To begin to help answer this question I'm going to share a quote that really resonates with me.

"I want my students [& children] to make the meaningful connection to math that I myself was able to make only as an adult" (Kulkin, 2016, p. 28).

When I first read this quote from Kulkin it was an eye opener for me. She accurately put into words my experiences and the feelings towards teaching math to my students and my own children. I want them to explore and see the beauty mathematics has to offer that I only came to conceptualize as an adult when I needed to understand the mathematics that I was teaching.

As a child [and many would say still today] I was a rule follower. As you can imagine in the math classes of the 90's this skill made for a good student. Teachers provided the formulas, I repeated them ad nauseam and spit out the answers. What I came to realize though, is that although I could follow any formula to find the 'one way' to a correct solution I didn't have a foundational understanding of the actual math I was doing. I didn't retain the math from unit to unit because it didn't hold any true meaning for me. It was simply something I needed to do to get good grades. I was provided with a roadmap that some mathematician somewhere had developed for finding something called a quadratic equation -- but what did that have to do with my life? The meaningful connections to math weren't there. The application, critical thinking, problem solving, and most importantly math reasoning opportunities weren't there because text books famously provided us with all of the information we need without having to look for it. To quote Dan Meyer, "what real world problem, that was worth solving, did you know all of the given information in advance?"

So, what's math got to do with it? Mathematics is found everywhere in the world around us. Take a moment to look around where you are now. Where do you see math? Maybe it's in the budget sitting in the pile of paperwork beside you, or coming from the kitchen as someone is baking a batch of muffins, or the unique designs of the flowers growing outside your window, or the complex designs of the construction site happening in your neighbourhood, or the math involved with your next renovation, or the schedule of your upcoming roadtrip. We often take for granted the math that is all around us. Math is everywhere and it is an important part of our lives.

Math problems are solved every day, not from textbooks, but in real life, and our children need to develop mathematical reasoning skills through hands on experiences. The phrase, 'less is more' can be applied to our math classrooms. "A growing set of data indicates that classroom practice currently is tailored to support students' execution of low level skills" (Hiebert et al., 2005, p. 18). For example, low level tasks involve memorizing and reproducing formulas without making connections to their meaning. Schools are moving away from activities that involve lower levels of cognitive demand (e.g., memorization and procedures without connections) and offering tasks with higher levels of cognitive demand (e.g., procedures with connections and doing mathematics). These are the changes that you are seeing and the 'differences' that you may be witnessing in your child's math work. Instead of asking students to repeatedly practice 10-15 questions using given formulas they may be given one or two complex problems requiring them to explore mathematical concepts or processes. Less is more!

Smith and Stein developed a chart outlining the "characteristics of mathematical tasks at four levels of cognitive demand." The images below are taken from their article, Selecting and Creating Mathematical Tasks: From Research to Practice. One takeaway that I notice from the examples provided is that my experiences with math classes as a student primarily involved the lower-level demand tasks. To me this really explains the shifts you may be witnessing in your child's math work. Educators now focus on providing students with activities that help them develop a conceptual and procedural understanding.

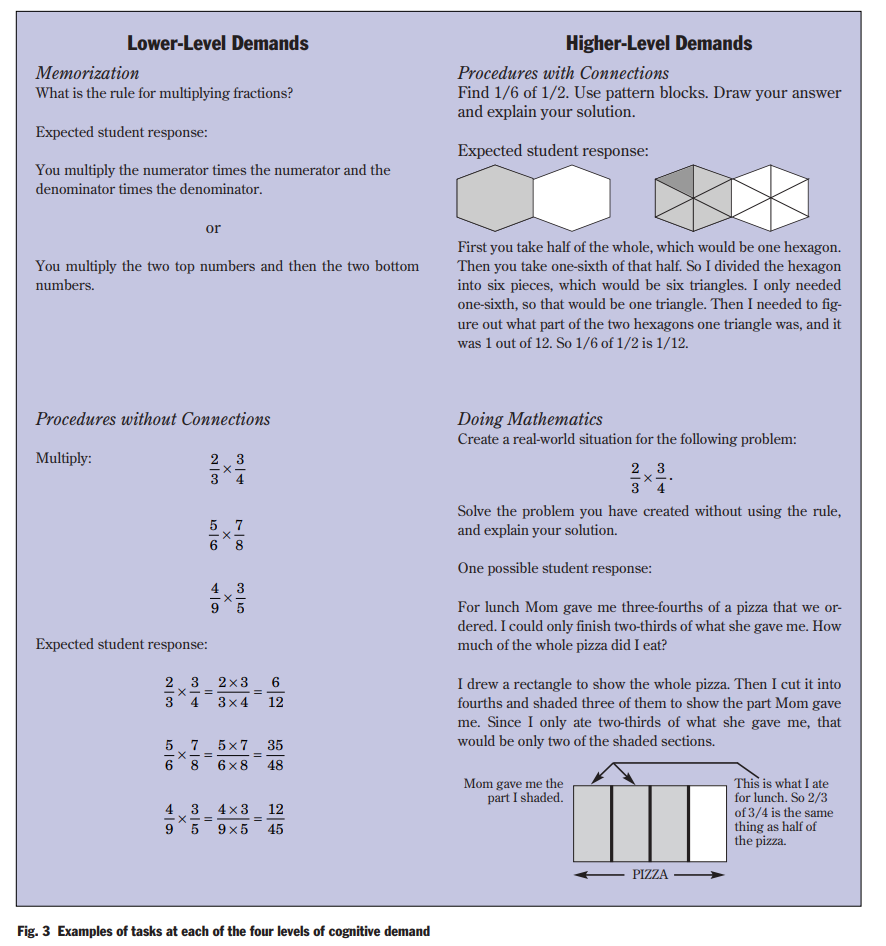
As a parent and educator, I'm excited to see the shift in tasks for my own children and students. Math isn't just about plugging arbitrary numbers into a formula anymore -- computers and those things glued to our hands [smart phones] can do that for us. Math needs to be about making connections, thinking critically, and being able to reason. Those are the lifeskills we need our children to have. To quote Kulkin again, as an educator [and mother], "I want my children to make the meaningful connection to math that I myself was only able to make as an adult" (2016, p. 28). This has become a passion for me -> helping individuals see the beauty and patterns in math around us.

References:

Hiebert, Stigler, J. W., Jacobs, J. K., Givvin, K. B., Garnier, H., Smith, M., Hollingsworth, H., Manaster, A., Wearne, D., & Gallimore, R. (2005). Mathematics Teaching in the United States Today (And Tomorrow): Results from the TIMSS 1999 Video Study. Educational Evaluation and Policy Analysis, 27(2), 111–132. https://doi.org/10.3102/01623737027002111

Smith, M, & Stein, M. (1998). “Selecting and Creating Mathematical Tasks: From Research to Practice.” Mathematics Teaching in the Middle School 3: 344–50.